Recapitulare pentru testul inițial
E.271. Suma a 3 numere pare consecutive este 600. Care este diferența dintre numărul cel mai mare și numărul cel mai mic?
Răspuns: Diferența cerută este 4.
Soluție:
a+(a+2)+(a+4)=600⇒a=198. Deci numerele noastre sunt 198, 200 și 202.
Diferența cerută este 202−198=4.
OBS: Nu era nevoie să aflăm numerele. Diferența cerută este (a+4)−a=4 și nu depinde de suma numerelor.
E.272. Dacă 2⋅a+3⋅b=13 și 2⋅b+3⋅c=19, calculați 4⋅a+8⋅b+3⋅c.
Indicații: Se înmulțește prima egalitate cu 2.
Soluție:
Înmulțim prima egalitate cu 2 și obținem 4⋅a+6⋅b=26.
Adunând la acest rezultat a 2-a egalitate, obținem 4⋅a+6⋅b+2⋅b+3⋅c=26+19, adică 4⋅a+8⋅b+3⋅c=45.
E.273. Calculați suma tuturor resturilor care se pot obține prin împărțirea unui număr la 11.
Soluție:
Prin împărțirea la 11 putem obține resturile 0,1,2,3,…,10.
S=(1+10)+(2+9)+(3+8)+(4+7)+(5+6)=11⋅5=55.
OBS: Suma putea fi calculată și cu formula lui Gauss:
S=1+2+3+…+10=(10⋅11):2=55.
E.274. Fie șirul de numere: 1,7,13,19,25,31,…. Aflați al 100-lea termen al șirului.
Soluție:
Numerele apar din 6 în 6 și încep cu 1, deci sunt de forma 6⋅k+1, cu k=0,1,2,3,….
- 1=6⋅0+1 (termenul 1);
- 7=6⋅1+1 (termenul 2);
- 13=6⋅2+1 (termenul 3);
...
Observăm că valoarea lui k este cu 1 mai mică decât poziția termenului în șir.
Așadar, termenului de pe poziția 100 îi corespunde k=99, deci numărul căutat va fi 6⋅99+1=595.
E.275. Determinați suma numerelor de forma abc, știind că 5⋅a+5⋅b+5⋅c=40 și 0<a<b<c.
Soluție:
Împărțind egalitatea dată la 5 obținem a+b+c=8. Ținând cont că 0<a<b<c, obținem:
- a=1,b=2,c=5⇒abc=125;
- a=1,b=3,c=4⇒abc=134.
Deci suma cerută este 259.
E.276. Câte numere de la 1 la 1000 conțin cifra 2 exact de două ori?
Soluție:
Avem un singur număr de două cifre: 22. Numerele de 3 cifre pot fi de forma:
- 22x, unde x=0,1,3,4…9 (9 numere);
- 2x2, unde x=0,1,3,4…9 (9 numere);
- x22, unde x=1,3,4…9 (8 numere);
În total avem 1+9+9+8=27 numere.
E.277. Ionel repară un gard în 2 ore, Vasile repară gardul în 3 ore și Gigel în 6 ore. Dacă lucrează împreună, în câte ore vor termina gardul?
Indicații: Calculăm câte garduri ar putea să repare fiecare în 6h.
Soluție:
Calculăm câte garduri ar putea să repare fiecare în 6h:
- Ionel, 6:2=3 garduri;
- Vasile, 6:3=2 garduri;
- Gigel, 1 gard.
Deci, dacă lucrează împreună, cei trei ar putea să repare 3+2+1=6 garduri în 6 ore. Adică un gard în 1h.
E.278. Într-un tren, Dan stă în al 7-lea vagon, numărat de la locomotivă, iar Gigel în al 13-lea vagon, numărat pornind de la ultimul vagon, și este într-un vagon mai apropiat de locomotivă decât Dan. Între ei sunt 3 vagoane. Câte vagoane are trenul?
Soluție:
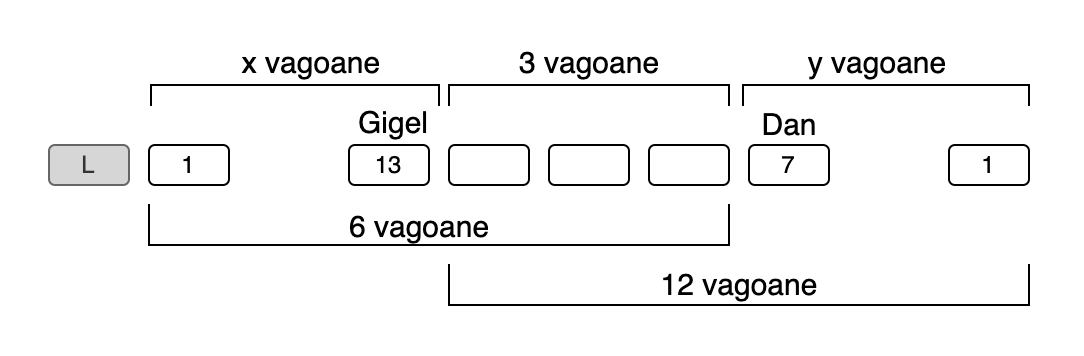
x+3=6⇒x=3;
y+3=12⇒y=9.
În total, trenul are x+3+y=15 vagoane.
E.313. Un om taie mai multe scânduri lungi cu fierăstrăul, făcând din ele bucăți mai scurte. Face 57 de tăieturi și obține 85 de bucăți. Câte scânduri erau la început?
Marcelina Popa (grupul profesorilor); Petre Bătrânețu (MateMaraton)
Indicații: Fiecare tăietură adaugă o nouă bucată de scândură.
Răspuns: 28 scânduri.
Soluție:
Fiecare tăietură adaugă o nouă bucată de scândură, Dacă inițial avem n scânduri, atunci:
- după o tăietură ⇒n+1 bucăți;
- după două tăieturi ⇒n+2 bucăți;
- ...
- după 57 tăieturi ⇒n+57 bucăți;
Dar n+57=85⇒n=28 scânduri.
E.320. Un melc urcă pe un stâlp cu înălțimea de 4 m, pornind de la baza acestuia. Cât timp soarele e pe cer, melcul urcă 70 cm, dar noaptea adoarme și alunecă 40 cm. În a câta zi ajunge melcul în vârful stâlpului?
Art, Matematică pentru excelență, 1/11
