Paralelism și perpendicularitate
Paralelism
A. Unghiuri determinate de două drepte și o secantă;
B. Criterii de paralelism:
- unghiuri alterne interne congruente;
- unghiuri corespondente congruente;
- unghiuri interne, de aceeași parte a secantei suplementare;
- unghiuri alterne externe suplementare;
C. Axioma paralelelor: Printr-un punct exterior unei drepte trece o singură dreaptă paralelă cu acea dreaptă.
Perpendicularitate
A. Drepte perpendiculare - două drepte concurente ce formează un unghi de
B. Distanța de la un punct la o dreaptă - lungimea perpendicularei duă din acel punct pe dreaptă.
C. Mediatoarea unui segment - perpendiculara construită prin mijlocul segmmentului.
D. Simetria față de o dreaptă
E.387. Arătați că suma măsurilor unghiurilor unui triunghi este egală cu
Indicații: Se construiește prin
E.391. Demonstrați că bisectoarele unei perechi de unghiuri alterne externe, determinate de două drepte paralele cu o secantă, sunt incluse în drepte paralele.
E.388. Arătați că bisectoarele a două unghiuri adiacente suplementare formează un unghi drept.
E.389. În figura alăturată cunoaștem că
E.392. Fie
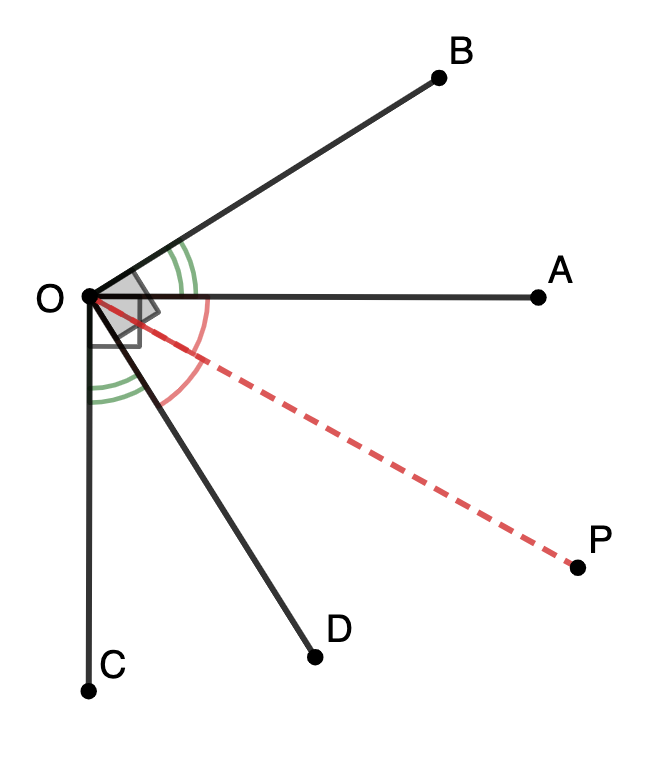
Din ipoteză
E.393. Triunghiul
E.394. Se consideră triunghiul
Comentariu: Daca luăm
E.390. În figura alăturată, dreptele
Indicații: Fie
Răspuns:
| Nume | CreatLa (UTC) |
|---|---|
| Tema4: Paralelism și perpendicularitate | 30-10-2024 13:44 |