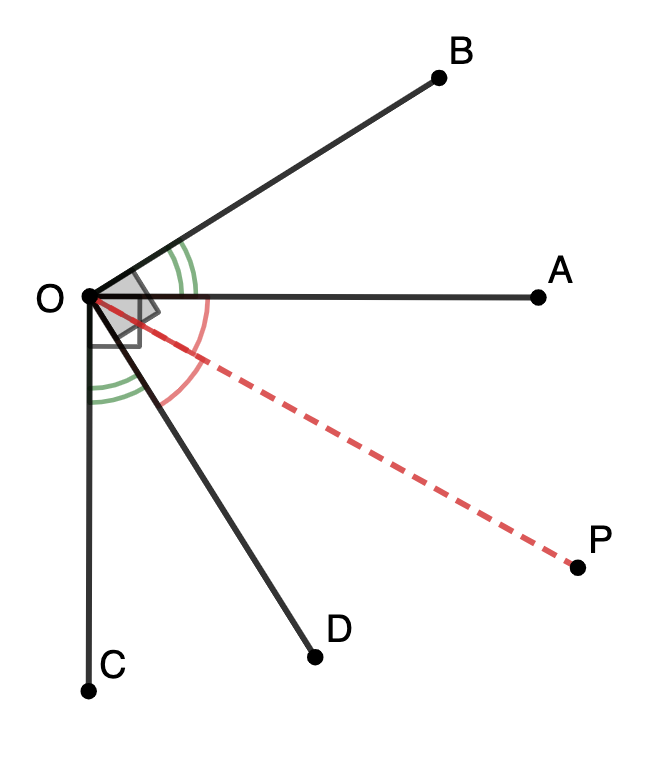
E.392. Fie A O B AOB A OB A O AO A O B B B C C C D D D O C ⊥ O A OC \bot OA OC ⊥ O A O D ⊥ O B OD \bot OB O D ⊥ OB O P OP OP A O D AOD A O D ∡ C O P = ∡ A O B + 24 ° \measuredangle COP=\measuredangle AOB+24 \degree ∡ COP = ∡ A OB + 24° A O B AOB A OB D O P DOP D OP
Olimpiadă, etapa locală, Covasna, 2020
Soluție:
D O C ^ = A O C ^ − A O D ^ = 90 ° − A O D ^ B O A ^ = B O D ^ − A O D ^ = 90 ° − A O D ^ } ⇒ D O C ^ = B O A ^ ( 1 ) .
\begin{rcases}
\widehat{DOC}=\widehat{AOC}-\widehat{AOD} = 90\degree - \widehat{AOD} \\
\widehat{BOA}=\widehat{BOD}-\widehat{AOD} = 90\degree - \widehat{AOD}
\end{rcases} \Rightarrow \boxed{\widehat{DOC}=\widehat{BOA}} \ (1).
D OC = A OC − A O D = 90° − A O D BO A = BO D − A O D = 90° − A O D } ⇒ D OC = BO A ( 1 ) . Din ipoteză C O P ^ = C O D ^ + 24 ° \widehat{COP}=\widehat{COD} + 24\degree COP = CO D + 24° C O D ^ + D O P ^ = C O D ^ + 24 ° ⇒ D O P ^ = 24 ° \widehat{COD}+\widehat{DOP}=\widehat{COD}+24\degree \Rightarrow \boxed{\widehat{DOP}=24\degree} CO D + D OP = CO D + 24° ⇒ D OP = 24°
O P OP OP A O D ^ ⇒ A O D ^ = 2 ⋅ D O P ^ \widehat{AOD} \Rightarrow \widehat{AOD} = 2 \cdot \widehat{DOP} A O D ⇒ A O D = 2 ⋅ D OP A O B ^ = ( 1 ) C O D ^ = 90 ° − A O D ^ = ( 2 ) 90 ° − 2 ⋅ D O P ^ ⇒ A O B ^ = 42 ° \widehat{AOB} \overset{(1)}{=}\widehat{COD} = 90\degree-\widehat{AOD} \overset{(2)}{=} 90\degree-2\cdot \widehat{DOP} \Rightarrow \boxed{\widehat{AOB}=42\degree} A OB = ( 1 ) CO D = 90° − A O D = ( 2 ) 90° − 2 ⋅ D OP ⇒ A OB = 42°