Exercițiul 281

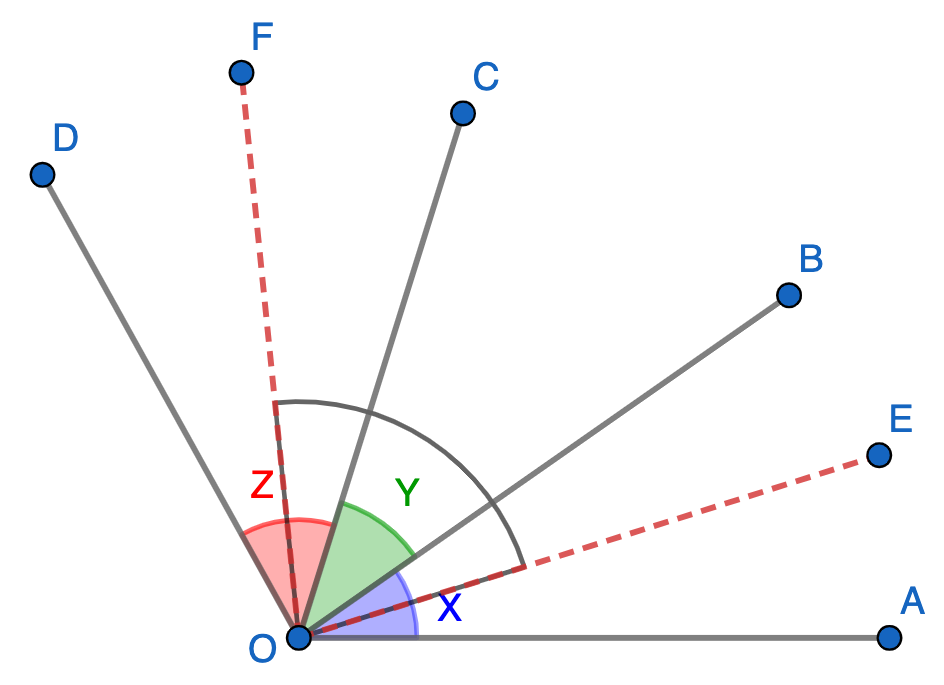
E.281. Fie punctele O,A,B,C,DO, A, B, C, D astfel încât BB se află în interiorul unghiului AOC,AOC, CC se află în interiorul unghiului BOD,BOD, m(∡AOD)=140°,m(\measuredangle AOD) = 140 \degree, b⋅m(∡AOB)=a⋅m(∡BOC)b \cdot m(\measuredangle AOB) = a \cdot m(\measuredangle BOC) și c⋅m(∡BOC)=b⋅m(∡COD),c \cdot m(\measuredangle BOC) = b \cdot m(\measuredangle COD), unde a,b,ca, b, c sunt numere prime distincte, astfel încât 7a+14b+2c=77.7a+14b+2c=77. Dacă OEOE este bisectoarea unghiului AOBAOB și OFOF este bisectoarea unghiului CODCOD, calculați măsura unghiului EOF.

Olimpiadă, etapa locală, Buzău, 2020
Răspuns | Soluție

Răspuns: EOF^=80°.\widehat{EOF}=80\degree.

Soluție:

7a+14b+2c=777a + 14b + 2c = 77
7(a+2b)+2c=77⇒c=77(a + 2b) + 2c = 77 \Rightarrow \boxed{c=7} (singurul nr. prim multiplu de 77).

7(a+2b)+14=777(a + 2b) + 14 = 77
7(a+2b)=63∣:77(a + 2b) = 63 \quad \mid :7
a+2b=9a + 2b = 9
aa este impar, prim și diferit de 7⇒a∈{3,5}.7 \Rightarrow a \in \{3, 5\}.
∙ Pentru a=3⇒b=3\quad \bullet \ \text{Pentru} \ a = 3 \Rightarrow b = 3, nu convine (sunt identice).
∙ Pentru a=5⇒b=2\quad \bullet \ \text{Pentru} \ \boxed{a = 5} \Rightarrow \boxed{b=2}.

Notând x=m(∡AOB)x = m(\measuredangle AOB), y=m(∡BOC)y = m(\measuredangle BOC), z=m(∡COD)z = m(\measuredangle COD), avem:

{2x=5y(1)7y=2z(2)x+y+z=140(3) \begin{cases} 2x=5y \quad (1) \\ 7y=2z \quad (2) \\ x+y+z=140 \quad (3) \end{cases}

Fiindcă în primele două relații avem valorile pentru 2x2x și 2z2z, înmulțim relația (3)(3) cu 22:
2x+2y+2z=2802x+2y+2z=280
5y+2y+7y=2805y + 2y + 7y = 280
14y=280⇒y=20.14y = 280 \Rightarrow \boxed{y=20}.

Revenind la relațiile (1)(1) și (2)(2) obținem x=50\boxed{x=50} și z=70\boxed{z=70}.

m(∡EOF)=x2+y+z2=25+20+35m(\measuredangle EOF) = \dfrac{x}{2} + y + \dfrac{z}{2} = 25+20+35, deci m(∡EOF)=80°\boxed{m(\measuredangle EOF)=80\degree}.