Exercițiul 280

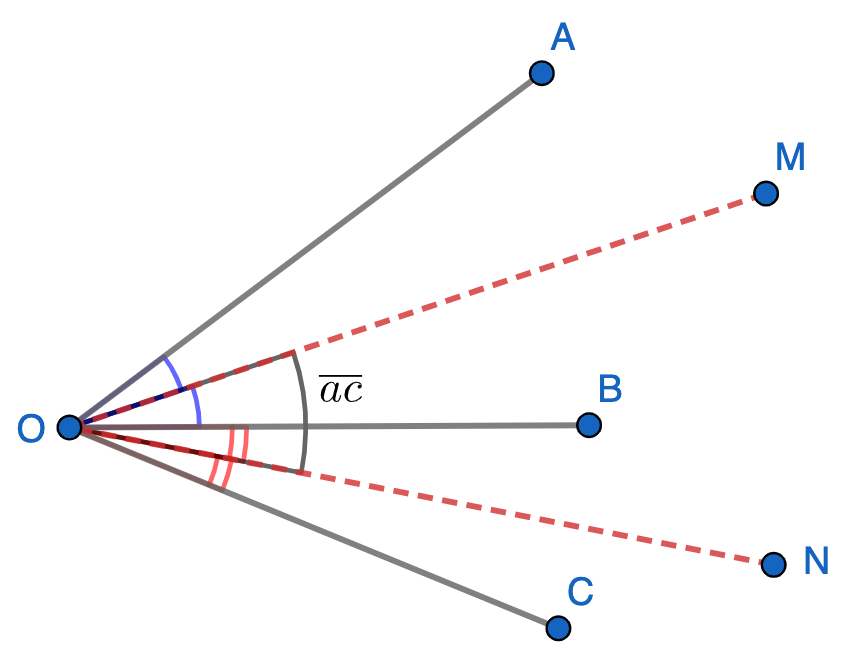
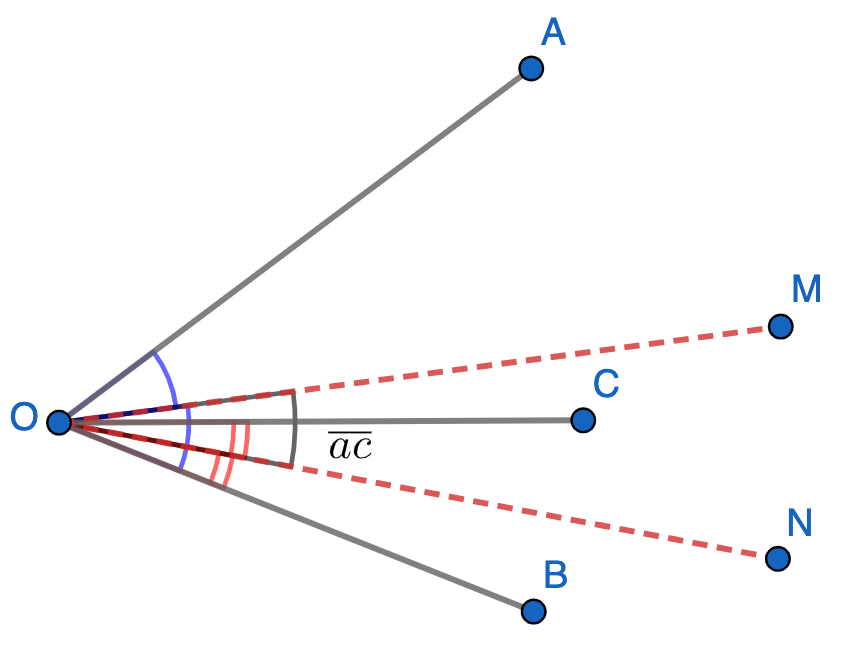
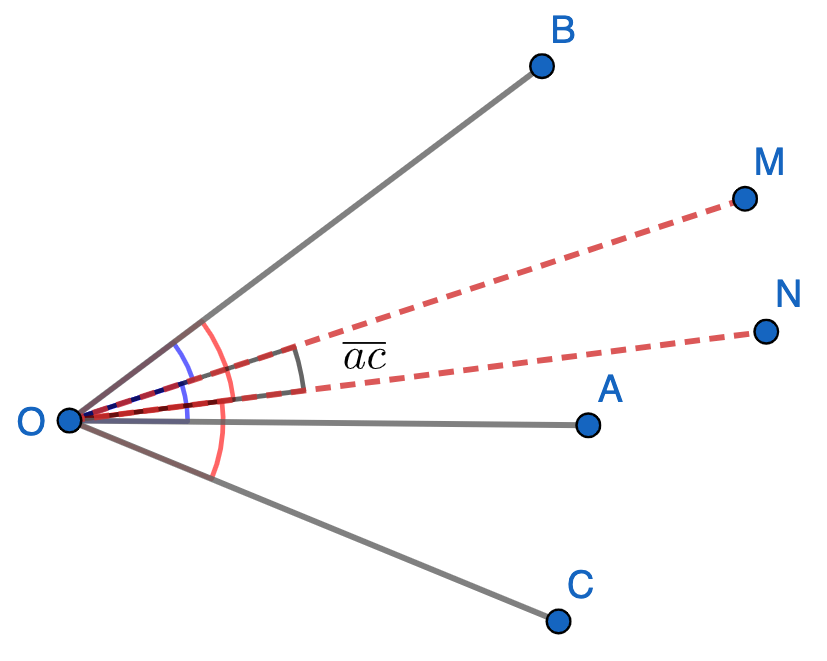
E.280. Se consideră unghiurile AOBAOB și BOC,BOC, astfel încât m(∡AOB)=ab‾°, m(∡BOC)=bc‾°m(\measuredangle AOB)=\overline{ab} \degree,~m(\measuredangle BOC)=\overline{bc} \degree și m(∡MON)=ac‾°,m(\measuredangle MON)=\overline{ac} \degree, unde [OM[OM este bisectoarea unghiului AOB, [ONAOB, ~[ON este bisectoarea unghiului BOC,BOC, iar a,ba, b și cc sunt cifre distincte în baza 10. Aflați valorile necunoscutelor aa, bb și cc.

Olimpiadă, etapa locală, Ialomița, 2020
Indicații (1) | Răspuns | Soluție

Indicații: Tratăm 33 cazuri:

  • MON^=MOB^+BON^;\widehat{MON}=\widehat{MOB} + \widehat{BON};
  • MON^=MOB^−BON^\widehat{MON}=\widehat{MOB} - \widehat{BON};
  • MON^=BON^−MOB^\widehat{MON}=\widehat{BON} - \widehat{MOB}.

Răspuns: abc‾∈{146,273}.\overline{abc} \in \{146, 273\}.

Soluție:

Caz 1:

MON^=MOB^+BON^\widehat{MON}=\widehat{MOB} + \widehat{BON}
ac‾=ab‾2+bc‾2\overline{ac} = \dfrac{\overline{ab}}{2} + \dfrac{\overline{bc}}{2}
2(10a+c)=10a+b+10b+c2(10a+c) = 10a + b + 10b + c
20a+2c=10a+11b+c20a+2c = 10a+11b+c
10a+c=11b10a+c=11b, imposibil pt. că Uc(10a+c)=cU_c(10a+c)=c și Uc(11b)=b.U_c(11b)=b.

Caz 2:

MON^=MOB^−BON^\widehat{MON}=\widehat{MOB} - \widehat{BON}
ac‾=ab‾2−bc‾2\overline{ac} = \dfrac{\overline{ab}}{2} - \dfrac{\overline{bc}}{2}
2(10a+c)=10a+b−10b−c2(10a+c) = 10a + b - 10b - c
20a+2c=10a−9b−c20a+2c = 10a -9b - c
10a+9b+3c=010a+9b+3c=0, imposibil pt. că a,b>0a,b>0, c≥0.c \geq 0.

Caz 3:

MON^=BON^−MOB^\widehat{MON}=\widehat{BON} - \widehat{MOB}
ac‾=bc‾2−ab‾2\overline{ac} = \dfrac{\overline{bc}}{2} - \dfrac{\overline{ab}}{2}
2(10a+c)=10b+c−10a−b2(10a+c) = 10b + c - 10a - b
20a+2c=9b+c−10a20a+2c = 9b +c - 10a
30a+c=9b30a+c=9b

Cum 9b≤9⋅9⇒30a≤81⇒a∈{1,2}.9b \leq 9 \cdot 9 \Rightarrow 30a \leq81 \Rightarrow a \in \{1,2\}.

∙ Pentru a=1⇒30+c=9b⇒b=4,c=6.\quad \bullet \ \text{Pentru} \ \boxed{a=1} \Rightarrow 30+c=9b \Rightarrow \boxed{b=4}, \boxed{c=6}.
∙ Pentru a=2⇒60+c=9b⇒b=7,c=3.\quad \bullet \ \text{Pentru} \ \boxed{a=2} \Rightarrow 60+c=9b \Rightarrow \boxed{b=7}, \boxed{c=3}.